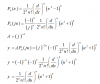با سلام
من موقع حل یک مسئله به معادله دیفرانسیل زیر رسیدم:
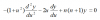
که با تغییر متغیرزیر:
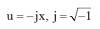
به این معادله میرسیم:
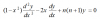
که جواب این معادله توابع لژاندرنوع اول و نوع دوم میباشد بنابراین داریم:
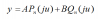
میخوام بدونم رابطه ی P[SUB]n[/SUB](ju) و Q[SUB]n[/SUB](ju) برحسب P[SUB]n[/SUB](u) و Q[SUB]n[/SUB](u) چیه؟ یا اصلا این توابع تعریف شده هستند؟ چه طوری تعریف میشن؟ نمودار تغییراتشون برحسب x چه طوریه؟کجا بی نهایت میشن کجا صفر؟ راه دیگه ای به جز تغییر متغیر برای این معادله وجود نداره؟ البته نه از راه سری یه جواب بر حسب توابع شناخته شده ای مثل لژاندر و... میخوام.
ممنون میشم اگه راهنماییم کنید.
با تشکر
من موقع حل یک مسئله به معادله دیفرانسیل زیر رسیدم:
که با تغییر متغیرزیر:
به این معادله میرسیم:
که جواب این معادله توابع لژاندرنوع اول و نوع دوم میباشد بنابراین داریم:
میخوام بدونم رابطه ی P[SUB]n[/SUB](ju) و Q[SUB]n[/SUB](ju) برحسب P[SUB]n[/SUB](u) و Q[SUB]n[/SUB](u) چیه؟ یا اصلا این توابع تعریف شده هستند؟ چه طوری تعریف میشن؟ نمودار تغییراتشون برحسب x چه طوریه؟کجا بی نهایت میشن کجا صفر؟ راه دیگه ای به جز تغییر متغیر برای این معادله وجود نداره؟ البته نه از راه سری یه جواب بر حسب توابع شناخته شده ای مثل لژاندر و... میخوام.
ممنون میشم اگه راهنماییم کنید.
با تشکر