::معماهاي رياضي::جهت شكوفايي استعداد شما

[mazoolagh]

خوب اون موضوع همنهشتي خيلي كار رو ساده كرد (هر چند خودم اول بهش دقت نكرده بودم و سئوال كردم:blush: )

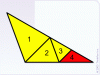
اينجوري خطوط برش نميتونن پيچيده باشن و در اين مثال مورب هم نميتونن باشن (چرا؟) - براي حلش شكل رو به 3 مربع كوچك 1*1 تقسيم كردم و حساب كردم براي اينكه 4 سطح مساوي از اين 3 تا بسازيم بايد از هر كدوم يك چهارمش رو برداريم و 3 تا يك چهارم رو هم كه خيلي راحت به ذهن تداعي شد كه چجوري بايد كنار هم بگذاريم.

خوب - حالا معماي بعدي!

 

[vahid_persian]

راه حلت کاملا اصولی بود . خوب حالا یکی دیگه معما طرح کنه

 

[mazoolagh]

مردي يك ششم عمرش رو در كودكي ميگذرونه - و بعد از اون يك دوازدهم از عمرش رو در جواني - بعد از طي يك هفتم ديگه از عمرش ازدواج ميكنه و پنج سال بعد از ازدواجش صاحب پسري ميشه كه وقتي سنش به نصف طول عمر پدرش ميرسه ميميره و پدرش هم 4 سال بعد ميميره.

اين مرد چند سال عمر كرده؟

 

[Huashan]

مردي يك ششم عمرش رو در كودكي ميگذرونه - و بعد از اون يك دوازدهم از عمرش رو در جواني - بعد از طي يك هفتم ديگه از عمرش ازدواج ميكنه و پنج سال بعد از ازدواجش صاحب پسري ميشه كه وقتي سنش به نصف طول عمر پدرش ميرسه ميميره و پدرش هم 4 سال بعد ميميره.

اين مرد چند سال عمر كرده؟

84 سال
اگه درسته بگین تا راه حل رو بنویسم

 

[vahid_persian]

y=(1/6)y+(1/12)y+(1/7)y+5+(y/2)+4 ==> y=84


البته آقا huashan هم به 84 رسیده بود و مطمئنا از همین راه رسیدن

 

[mazoolagh]

راه ساده تري از حل معادله درجه يك هم هست

 

[vahid_persian]

راه ساده تري از حل معادله درجه يك هم هست

بالاخره جواب همون 84 میشه دیگه نه؟حالا به هر روشی...

 

[mazoolagh]

خوب راه ساده تر اينه كه سن اين مرد بايد هم به 7 و هم به 6 و هم به 12 قابل قسمت باشه (6 بخاطر 12 ميره كنار).

اولين مضرب مشترك (همون ك.م.م) 7 و 12 ميشه 7*12=84 و مضرب مشترك بعدي هم 168 ميشه كه از محدوده عمر انسان خارج هست پس همون 84 درسته!

 

[Huashan]

خوب راه ساده تر اينه كه سن اين مرد بايد هم به 7 و هم به 6 و هم به 12 قابل قسمت باشه (6 بخاطر 12 ميره كنار).

اولين مضرب مشترك (همون ك.م.م) 7 و 12 ميشه 7*12=84 و مضرب مشترك بعدي هم 168 ميشه كه از محدوده عمر انسان خارج هست پس همون 84 درسته!

جالب بود ,
من اینطوری حسابش کردم
زمانی که مرد با پسرش زندگی می کنه , که معادلش می شه X/2

و زمانی که مرد بدون حضور پسرش زندگی می کنه که می شه , X/12+4+5+X/6+X/7

خب با قرار دادن این دو معادله مساوی هم جواب بدست میاد , که می شه همون معادله ای که دوستمون بدست آورد

 

[mazoolagh]

يك مثلث رو در نظر بگيرين كه يك زاويه منفرجه داشته باشه - مثل شكل پيوست:

ميخواهيم اين مثلث رو به مثلثهايي تقسيم كنيم كه همگي حاده باشن. همينطور كه در شكل ميبينين مثلث شماره 4 منفرجه است و معلوم ميشه كه بايد شگرد خاصي براي تقسيم استفاده كرد.

حالا شما بگين اين شگرد چي هست و حداقل چند مثلث بايد باشن؟

 

[Reza_A]

ابتدا مربع DBEG را درون مثلث قرار می دهیم و ارتفاع AF را رسم می کنیم. سپس نقاط C و E و G را کمی به سمت نقطه F حرکت می دهیم تا زوایای قائمه تبدیل به حاده شوند. حطوط قرمز رنگ نشاندهنده خطوط برشند.
همونطورکه مشخصه با این روش 7 مثلث ایجاد میشه.



[

 

[mazoolagh]

اينطور كه از استدلال شما برداشت كردم اون پنج ضلعي كه وسط ساخته ميشه بايد طوري باشه كه هر 5 مثلث درونش حاده باشن و هميشه ميشه يك 5 ضلعي رو به اين صورت تقسيم كرد. درست فهميدم؟

 

[Reza_A]

اون روش رسمی که گفتم برای این بود که برای پنج ضلعی حاصل، این مساله تضمین شده باشه. توی شکل بالا زوایای EBC و GDC و BCA و DCA قائمه اند که با کمی حرکت دادن نقطه C بسمت نقطه F تبدیل به حاده خواهند شد. زاویه ECG هم با توجه به مربع بودن EBDG حاده است و سایر زوایا نیز حاده می باشند که با کمی حرکت دادن نقاط C و G و E بسمت نقطه F (حرکت در حدی که زوایای قائمه ذکر شده تبدیل به حاده شوند، یعنی به اندازه "اپسیلون") حاده باقی خواهند ماند.
وگرنه الزاما برای هر پنج ضلعی نمیشه این کارو کرد. مثلا این:


راستی! دستتون درد نکنه بخاطر مساله ها و معماهای خوبتون.

 

[mazoolagh]

براي دوستاني كه مايل هستن:

اثبات نياز به 7 مثلث و چگونگي روش تقسيم توسط والاس مانهايمر در سال 1960 ارائه شده. پايه استدلال بطور خلاصه بشرح زير هست:

تقسيم رو از راس زاويه منفرجه شروع ميكنيم. خطي كه از اين راس كشيده ميشه نميتونه به ضلع مقابل برسه چون يا يك مثلث حاده و يك مثلث منفرجه داريم (كه مسئله رو به تكرار ميكشونه) يا 2 مثلث قائم الزاويه (كه جواب نيستن)

پس اين خط بايد جايي داخل مثلث با خطوط تقسيم ديگه برخورد كنه. تعداد اين خطوط تقسيم بايد حداقل 5 تا باشه تا امكان حاده بوده تمام زوايا حاصل بشه. بنابراين يك 5 ضلعي خواهيم داشت و 2 مثلث كنار كه جمعا" ميشه 7 تا.

شكلي كه جناب reza گذاشتن كاملا" گويا هست - همينطور كه ميبينين تسلط و تبحر ايشون كاملا" مشخص و بينياز از تعريف هست.

 

[mazoolagh]

چهار متحرك A , B , C , D روي چهار گوشه مربعي به ضلع يك ايستاده اند.
در لحظه t=0 اين چهار متحرك به سمت هم حركت ميكنند: A به سمت B - B به سمت C - C به سمت D و D به سمت A و با تغيير موقعيت هر هدف ، متحرك به سمت هدف متوجه خواهد شد.

1- مسير حركت چيست؟
2- نقطه برخورد كجاست؟
3- هر متحرك از زمان شروع تا زمان برخورد چه مسافتي را ميپيمايد؟

 

[vahid_persian]

چهار متحرك A , B , C , D روي چهار گوشه مربعي به ضلع يك ايستاده اند.
در لحظه t=0 اين چهار متحرك به سمت هم حركت ميكنند: A به سمت B - B به سمت C - C به سمت D و D به سمت A و با تغيير موقعيت هر هدف ، متحرك به سمت هدف متوجه خواهد شد.

1- مسير حركت چيست؟
2- نقطه برخورد كجاست؟
3- هر متحرك از زمان شروع تا زمان برخورد چه مسافتي را ميپيمايد؟

1- فکر می کنم به شکل زیر تقریبا



2- اگر 4 تا نقطه باشند هیچ کجا به هم برخورد نمی کنن ولی اگر بحث فزیکی باشه و جرم تعریف بشه برا متحرک ها مرکز به هم می خورن .
3-اگر نقطه باشن بی نهایت

اگر جوابام درستن بگین تا توضیح بدم

 

[mazoolagh]

1- فکر می کنم به شکل زیر تقریبا
مشاهده پیوست 12608


2- اگر 4 تا نقطه باشند هیچ کجا به هم برخورد نمی کنن ولی اگر بحث فزیکی باشه و جرم تعریف بشه برا متحرک ها مرکز به هم می خورن .
3-اگر نقطه باشن بی نهایت

اگر جوابام درستن بگین تا توضیح بدم

1- شكل درسته
2- بهم ميرسن چه مادي باشن و چه نباشن
3- مسير طول معين داره و قابل محاسبه است

 

[Reza_A]

جناب mazoolagh ! خیلی شرمنده می کنید.

زحمت قسمت اول رو که آقا وحید کشیدند. دستشون درد نکنه.

مکان برخورد مرکز مربع، و مسافت طی شده توسط هر نقطه برابر با طول یک ضلع مربع (یک) است.



فرض می کنیم که مربع اصلی، مربع آبی رنگ ABCD باشد. پس از زمان کوتاه dt ، هریک از ذرات به اندازه a حرکت خواهد کرد و به رئوس مربع قرمز رنگ منتقل خواهد شد. مربع حاصل، مانند مربع آبی رنگ اما با اضلاع کوچکتر است. ذرات قرار گرفته در هریک از رئوس مربع جدید مجددا به اندازه a حرکت خواهند کرد و مربع کوچکتر سیاهرنگ را تشکیل خواهند داد. به این ترتیب اضلاع مربع کوچک و کوچکتر خواهند شد تا به صفر برسد.
اگر ضلع مربع آبی رنگ برابر با یک باشد، با توجه به کوچک بودن a ، ضلع مربع قرمز رنگ برابر با 1-a و ضلع مربع سیاهرنگ برابر با (1-a)-a=1-2a خواهد شد. بنا براین میزان کاهش اندازه ضلع مربع جدید نسبت به مربع اولیه همواره برابر خواهد بود با مسافت طی شده توسط ذره. بنابراین پس از آنکه ذره مسافت 1 را طی کند اضلاع مربع برابر با صفر خواهند شد و ذرات بهم برخورد می کنند.
با توجه به شکل می توان فهمید که مرکز تمامی مربع ها بر مرکز مربع اولیه منطبق است و از این رو وقتی طول ضلع مربع برابر با صفر شود، تمامی رئوس مربع در مرکز قرار خواهند گرفت.
این مساله با توجه به تقارن مساله نیز قابل درک است.

 

[mazoolagh]

ضمن اينكه از جناب وحيد (و ديگر دوستان) خواهش ميكنم كه كه معادله رياضي مسير رو تعيين كنن ميخواستم نظر جمع رو هم در مورد روش جالبي كه جناب رضا مطرح كردن بدونم.

 

[vahid_persian]

با توجه به شکلی که آقا رضا گفتند من فکر می کنم جواب مساله به صورت زیر قابل محاسبه باشه

مشاهده پیوست image.bmp


فرمول :
مشاهده پیوست 1.bmp

با توجه به این که :
مشاهده پیوست 2.bmp


ولی خوب جواب نهاییش رو بدست نیاوردم .